Beginner's Guide
Celestial Sphere
Understanding the Celestial Sphere
A basic understanding of our celestial sphere is necessary to know the sky, how the stars move, why the moon and planets are only seen in only a relatively small path in the sky, and how we mathematically designate the locations of the stars.
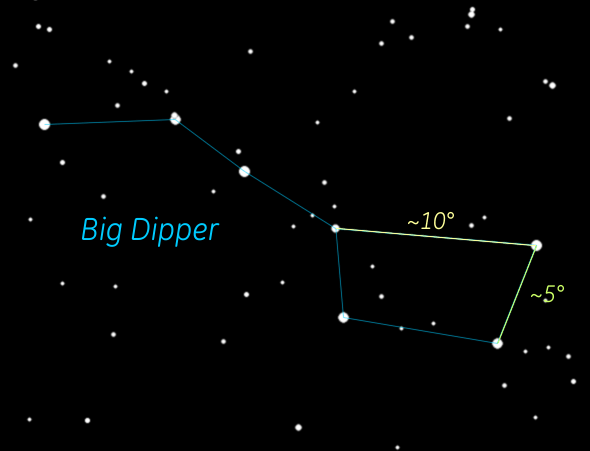
But a fundamental concept you need to know is what is a degree ( ° ) as in geometry. A circle has 360 degrees. When we look up into the sky we're seeing half of the sphere (horizon to horizon) which is half of a circle so 180°. From the horizon to the zenith (the point directly overhead) is 90° (aka right angle). As you can see from the image of the Big Dipper, you can use 3 of its stars to gauge smaller angles, in this case 5 and 10 degrees. And to give you an idea of a single degree, the full moon in the sky is about ½°.
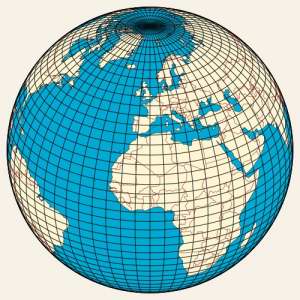
To understand celestial coordinates it is helpful to review the coordinate system we use for the Earth called the Geographic coordinate system. The reference lines we use are latitude and longitude. Latitude lines run east/west whereas longitude lines run north/south. Latitude lines are parallel and are natural because our rotating sphere dictates those lines. The axis of our rotation runs from the north pole to the south pole. Directly in the middle of that sphere we call the equator and that is designated as 0°. Latitude lines to the north are designated as degrees north (i.e., 15°N). An example of a line to the south would be shown 15°S.
Longitude lines go north to south. They are not parallel because they intersect at the north and south poles. But where is the zero line? Unfortunately there is no "natural" line. But we do have a zero line, 0°, and it's called the Prime Meridian (aka Meridian of Greenwich) because the line runs right through the Royal Observatory in Greenwich, London, England. It was the first one used and within a few years so many were using it as the reference, it was selected as the standard. Lines of longitude are designated either east or west based on their position relative to the Prime Meridian.
But we almost always need more precision than a single degree. Decimals can be used, but more often degrees are divided into minutes and seconds.
Just like a clock there are 60 minutes in a degree and 60 seconds in a minute. Our MAS Observatory in New Berlin, WI, has coordinates:
Latitude: N42° 58' 07.57"
Longitude: W88° 08' 53.89"
' is the symbol for minutes, " for seconds.
Celestial Coordinates
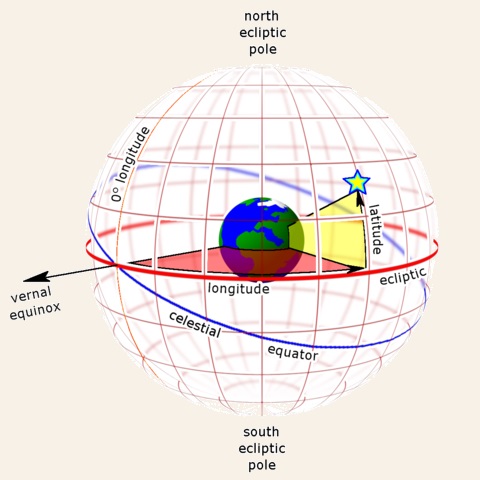 As the picture to the left shows, the celestial grid is very much identical to the terrestrial grid with latitudes and longitudes. It's as if the
terrestrial grid has just been projected onto the sky.
Celestial coordinates, however, are designated with Declination and Right Ascension, often abbreviated as Dec and RA. Dec is
analogous to latitude; RA to longitude. Every object in the sky has those two numbers which give its location.
As the picture to the left shows, the celestial grid is very much identical to the terrestrial grid with latitudes and longitudes. It's as if the
terrestrial grid has just been projected onto the sky.
Celestial coordinates, however, are designated with Declination and Right Ascension, often abbreviated as Dec and RA. Dec is
analogous to latitude; RA to longitude. Every object in the sky has those two numbers which give its location.
Declination (Dec) values are almost identical to latitude values, but instead of the N or S indicators for north or south of the equator, the range goes from -90° (south celestial pole) to 0° to +90 (north celestial pole.)
Right Ascension (RA) values, however, are different because they're specified in hours, minutes, and seconds. The range of values goes from 0h 0m 0s to 23h 59m 59s - 24 hours. At the equator in the celestial grid, 1 hour of RA equals 15°. So 15° times 24 = 360°.
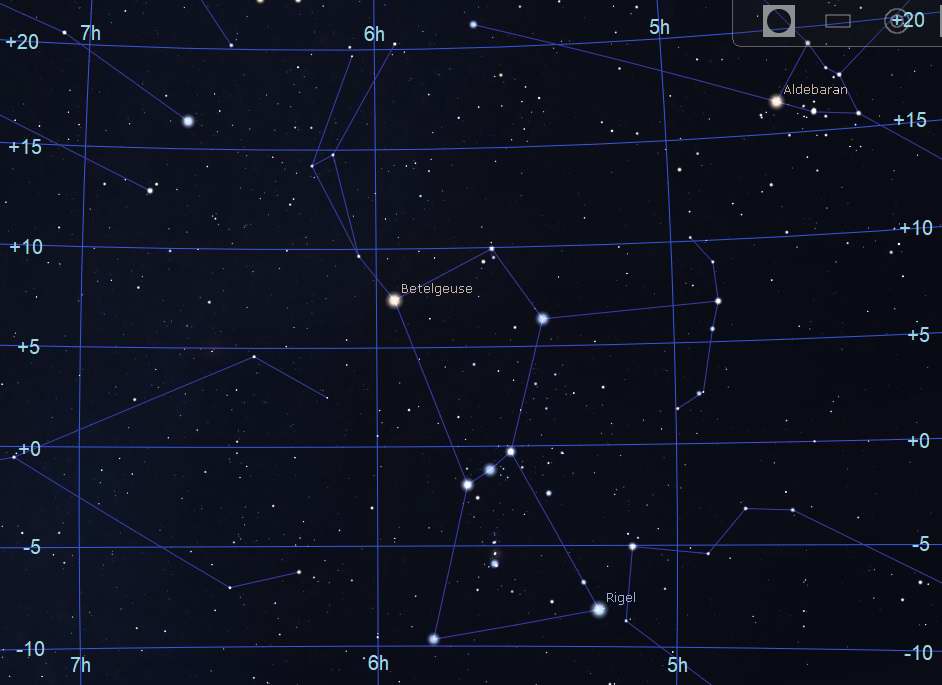
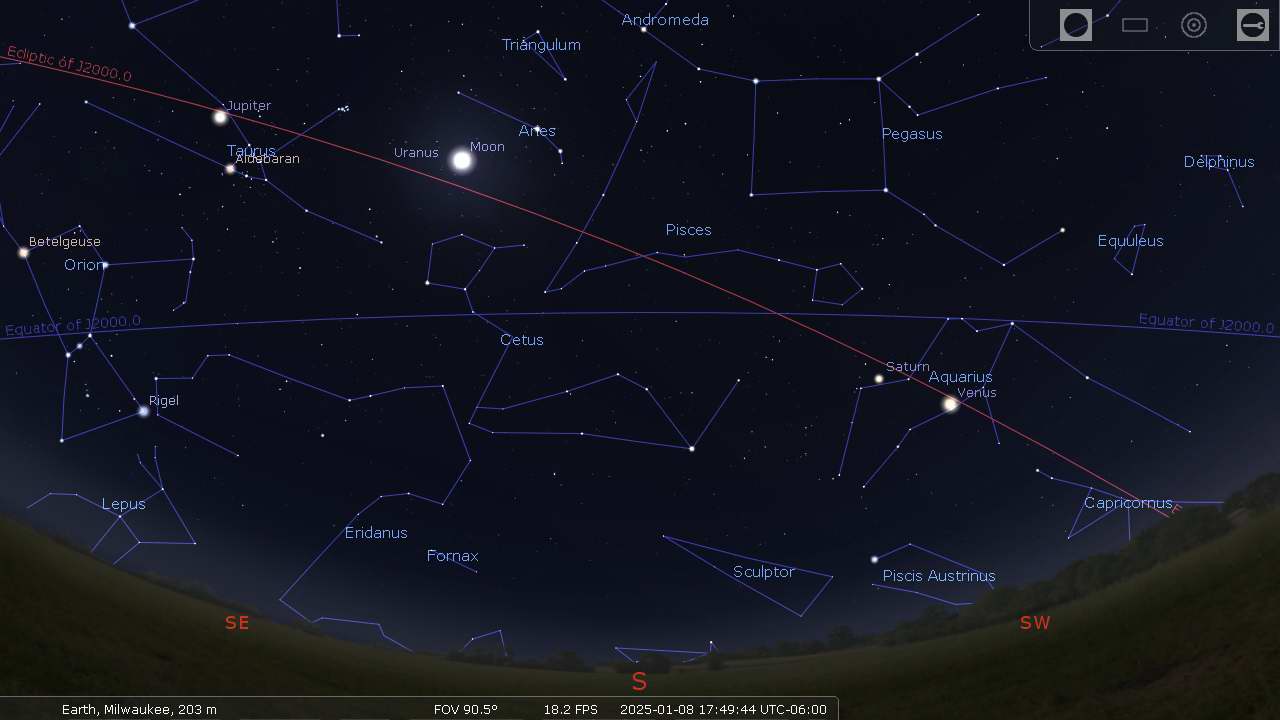
Above is the area of sky around the constellation Orion with the grid lines and values shown. Look at the following star coordinates against that map to see how they match.
| Name | Bayer Design | Dec | RA |
|---|---|---|---|
| Betelgeuse | α Orionis | +7° 24' 25" | 5h 55m 10s |
| Rigel | β Orionis | -8° 12' 06" | 5h 13m 32s |
| Aldebaran | α Tauri | +16° 30' 33" | 4h 35m 55s |
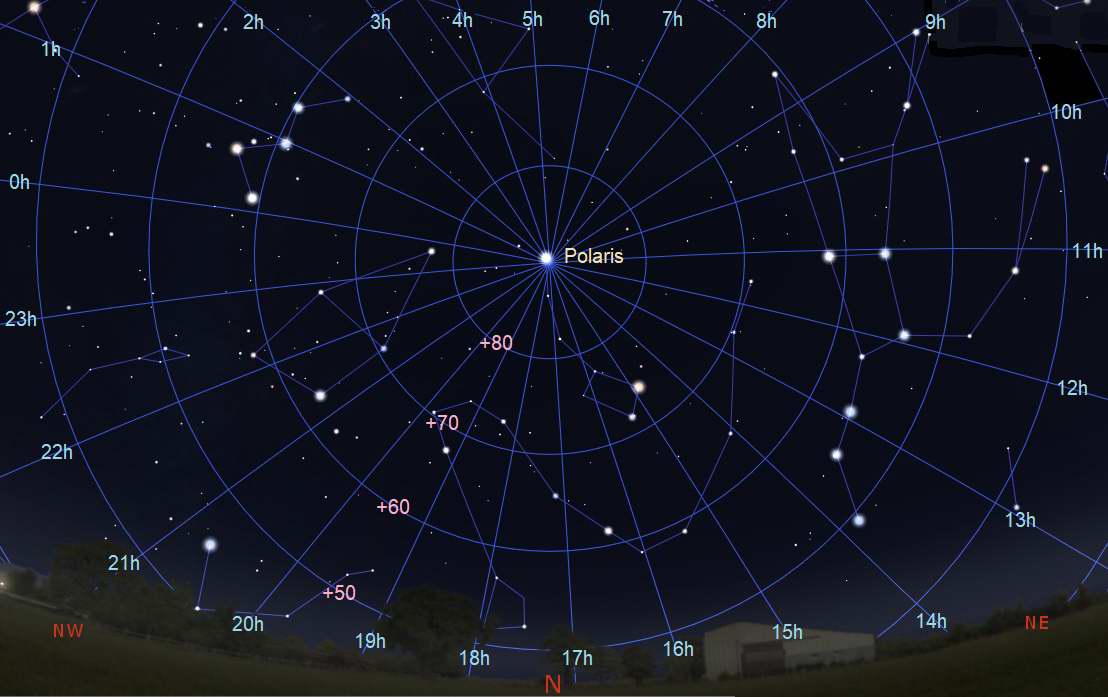
Sky looking directly North showing the RA and Dec lines.
 When you look up into the night sky and watch the motions of the moon,
planets, and stars, you see them rising in the east and continually moving
to the west where they will set. But that doesn't adequately describe the
stars that are far north on the celestial sphere. Here you will find the
circumpolar stars. These stars never rise and never set so they are always above the horizon.
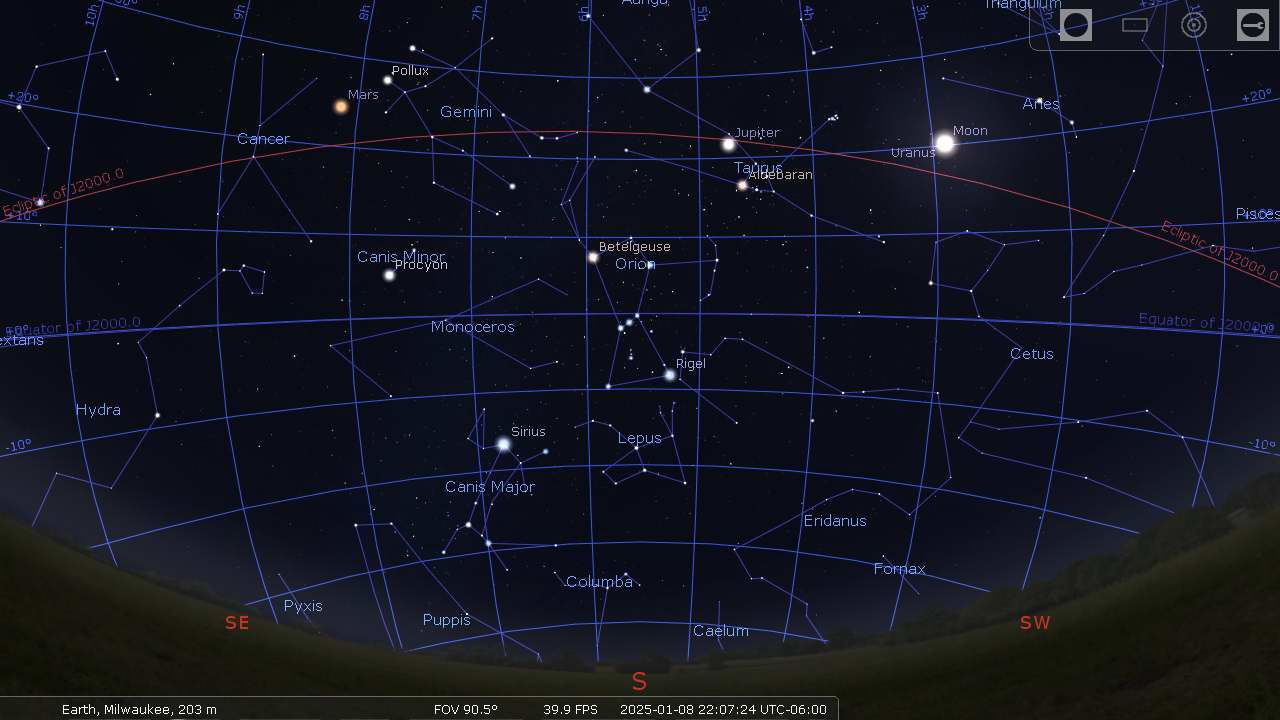
The image to the right shows the circumpolar region looking straight north.
The animation shows a complete rotation in just 20 seconds. It takes 24 hours for that to happen in the real sky.
Click/Tap here or on the image for a larger view.
When you look up into the night sky and watch the motions of the moon,
planets, and stars, you see them rising in the east and continually moving
to the west where they will set. But that doesn't adequately describe the
stars that are far north on the celestial sphere. Here you will find the
circumpolar stars. These stars never rise and never set so they are always above the horizon.
The image to the right shows the circumpolar region looking straight north.
The animation shows a complete rotation in just 20 seconds. It takes 24 hours for that to happen in the real sky.
Click/Tap here or on the image for a larger view.
The circle of stars that are circumpolar depend on the observers latitude. In the picture we are showing the view from Milwaukee which is at 43°. That also means that the North Star (Polaris) is 43° above the horizon.
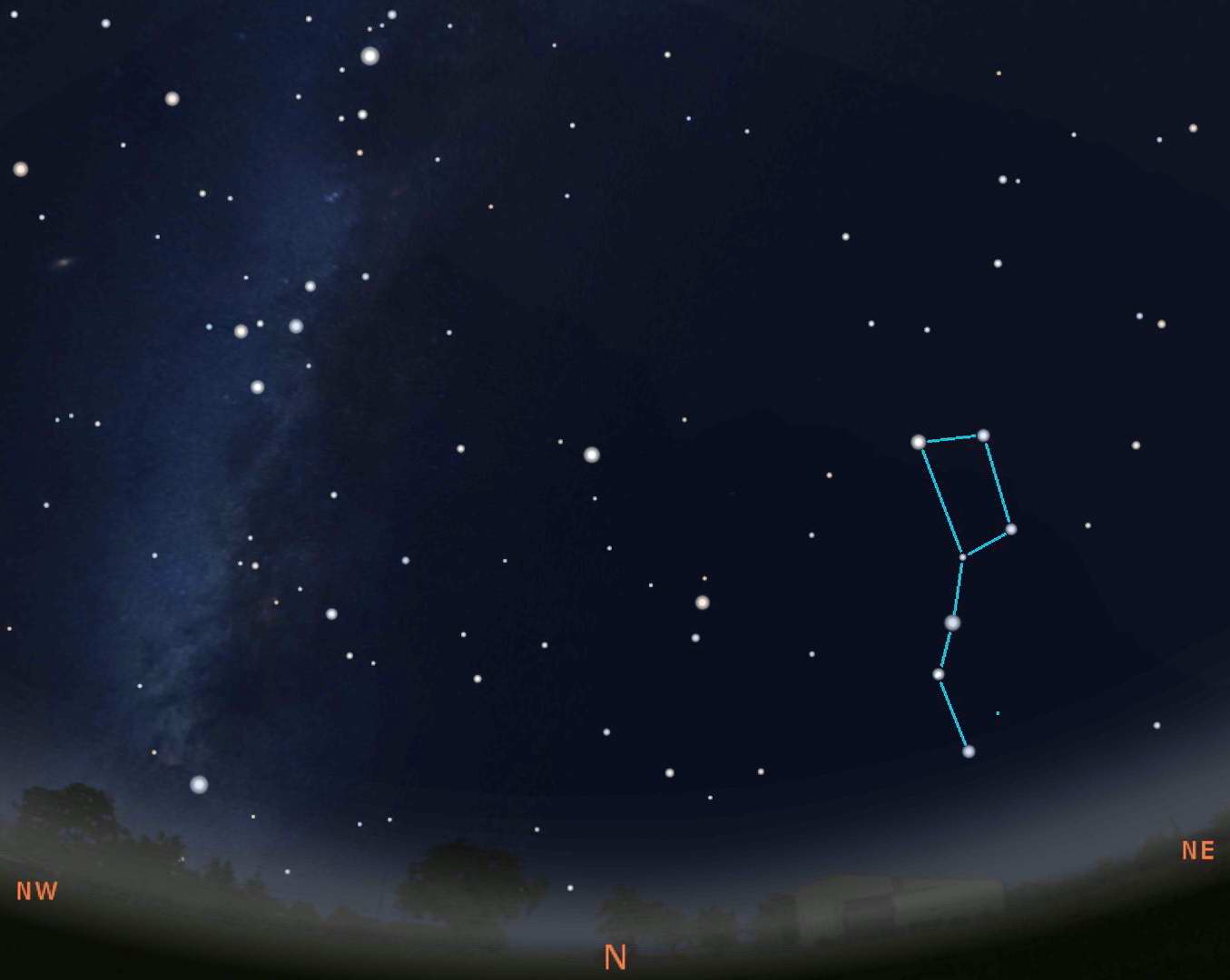
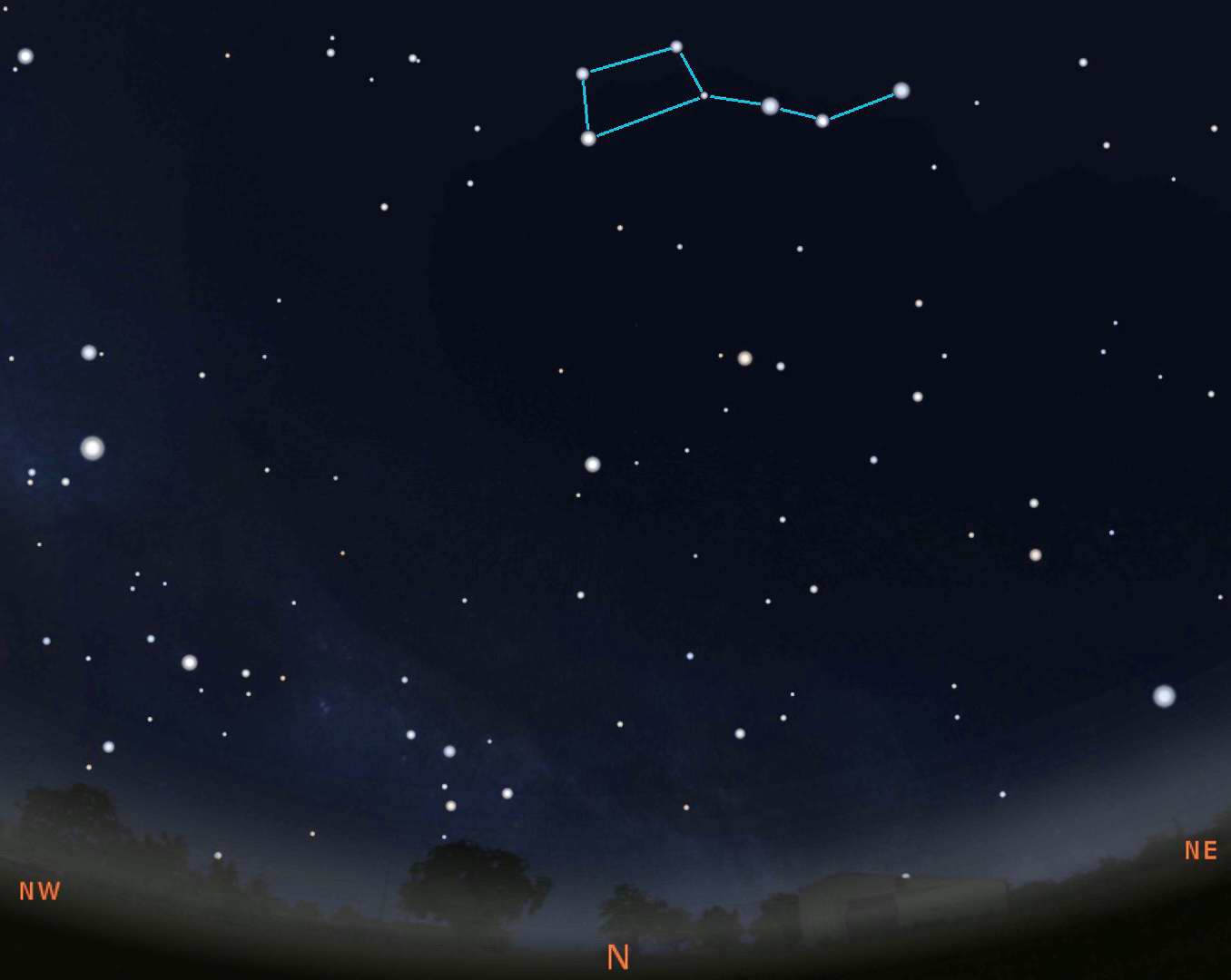
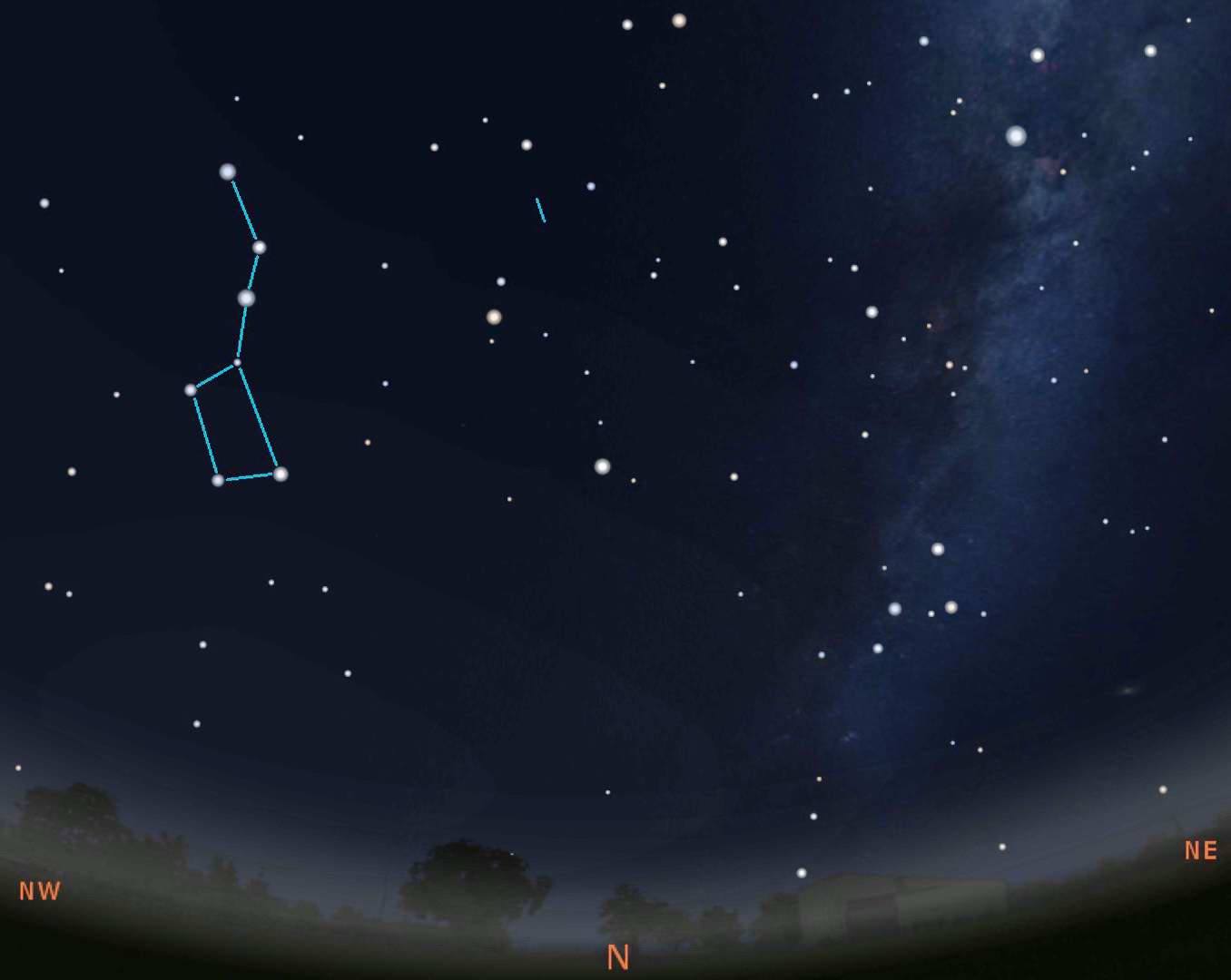
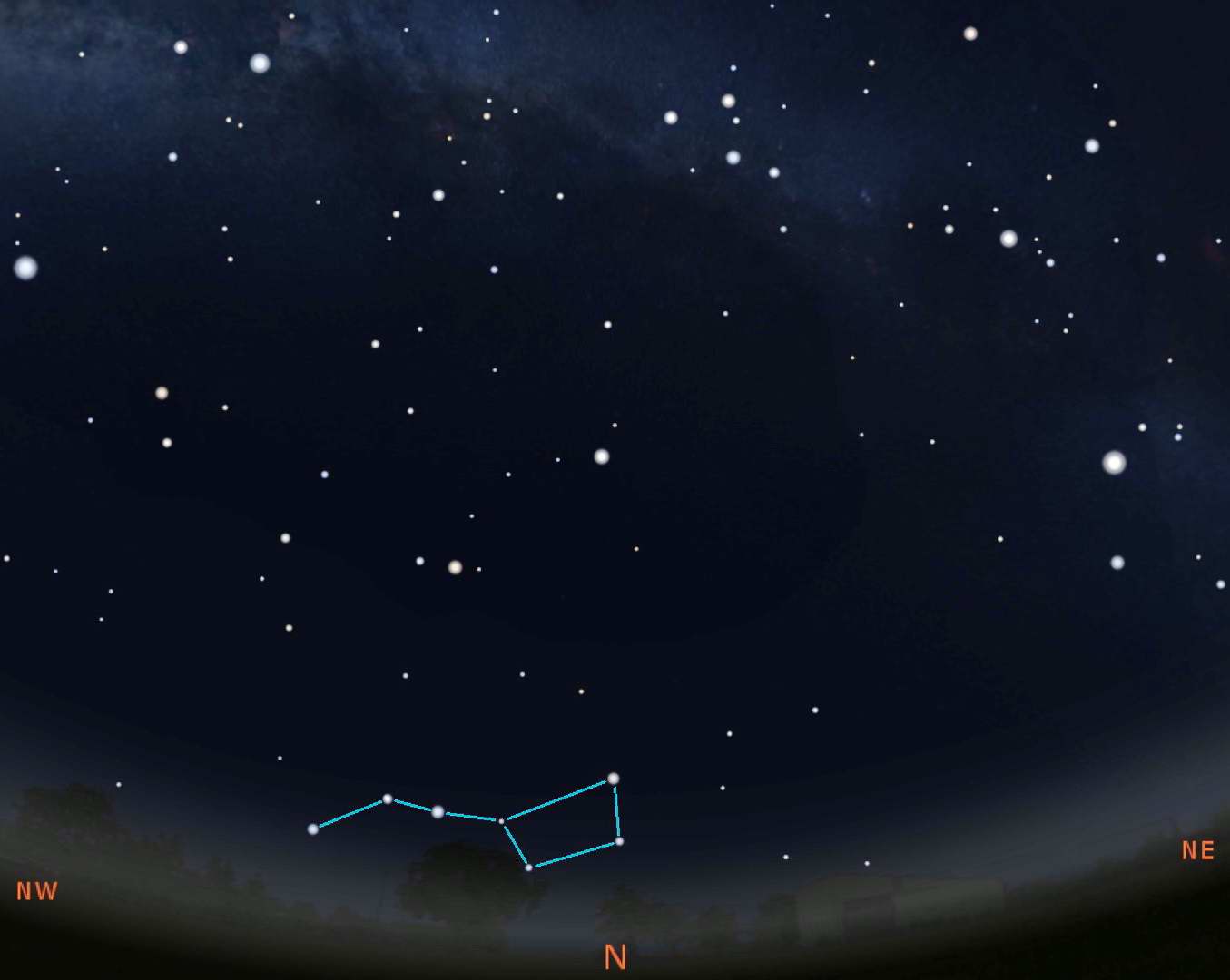
The Big Dipper Calendar and Clock
As you've just seen above, the stars that are circumpolar never set so they can be seen all year long and any time of night, assuming your horizon is good enough. The stars of the Big Dipper can be used as both a calendar and a 24 hour clock. Below we show 4 images of the sky looking directly north during the early evening of the 4 seasons.
The skies are about what you'd see at 9:00PM local time (note: not daylight savings) on January 20 (Winter), April 20 (Spring), July 20 (Summer), and October 20 (Autumn). The images above are for Milwaukee so it would be exactly what you'd see. But since the sky is always rotating, you can "see" the Big Dipper at this same location anytime of the year. Taking the Winter position shown, you will see that on December 20 at 11:00PM, November 20 at 1:00AM, October 20 at 3:00AM, etc. We put see in quotes because the Big Dipper will be at that position, but it will be daylight so you really can't see it.
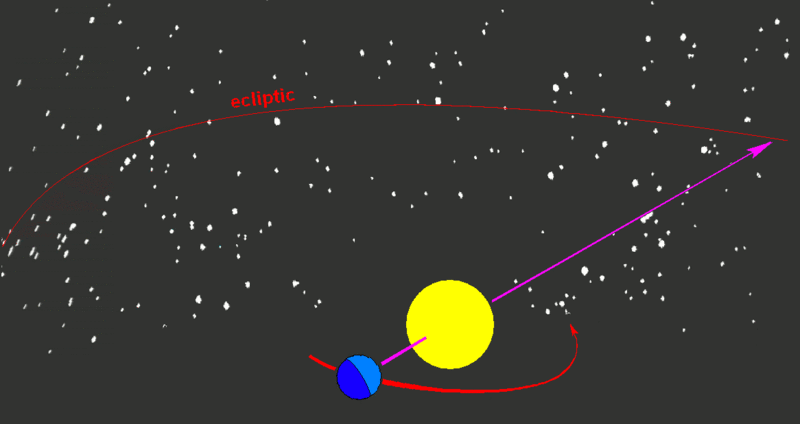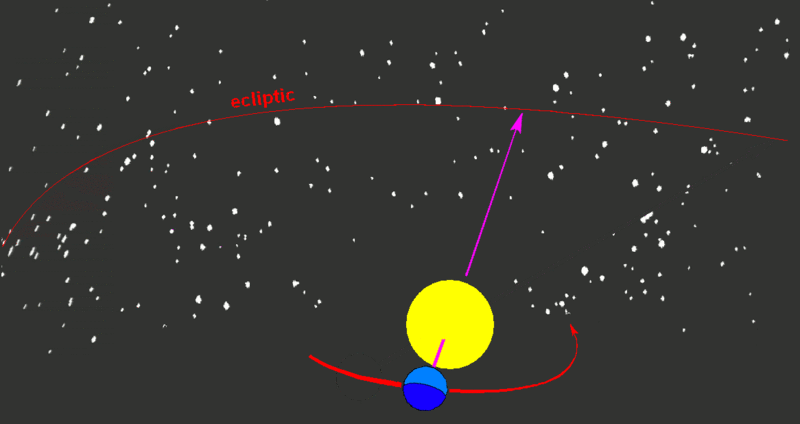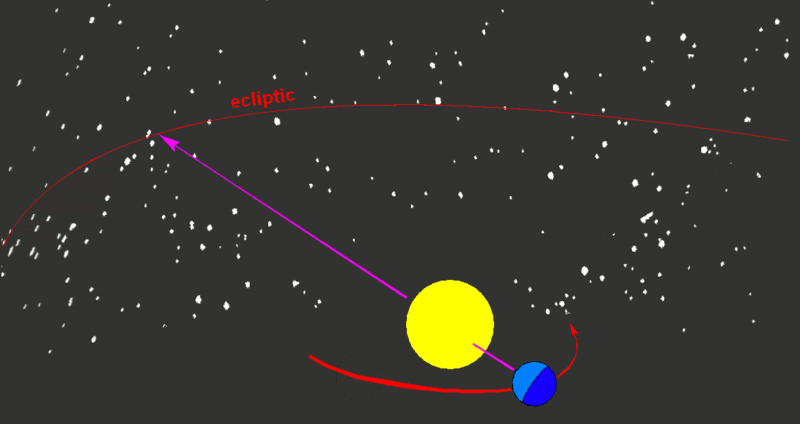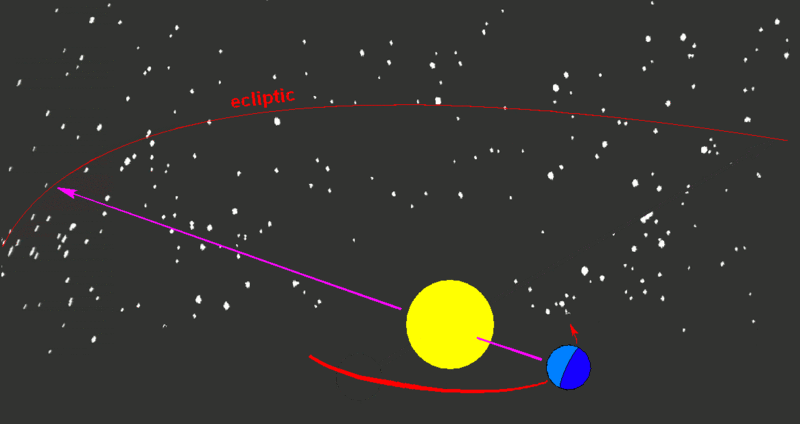
Ecliptic Path
Celestial sphere with Earth's celestial pole up with Ecliptic path at angle. Wikipedia Commons.

The plane of Earth's orbit projected in all directions forms the reference plane known as the ecliptic. Wikipedia Commons.
 We hope we have shown the motions
of the stars and how we designate the coordinates to be relatively straightforward. But we need to add some
complexity because you need to understand the ecliptic path.
We hope we have shown the motions
of the stars and how we designate the coordinates to be relatively straightforward. But we need to add some
complexity because you need to understand the ecliptic path.
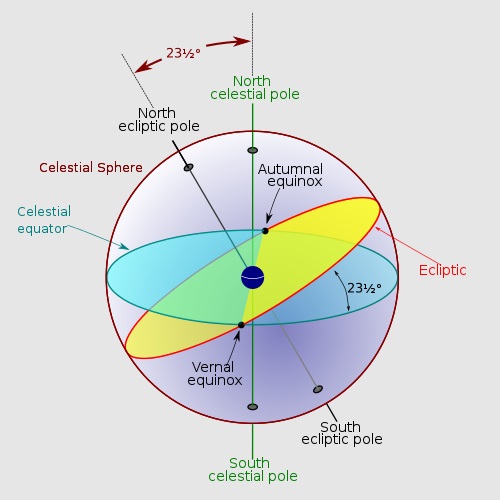
The ecliptic is the plane of Earth's orbit around our Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic against the background of stars. Simple enough. However, this path does not correspond with the celestial equator because the Earth is tilted in its orbit by 23.4°.
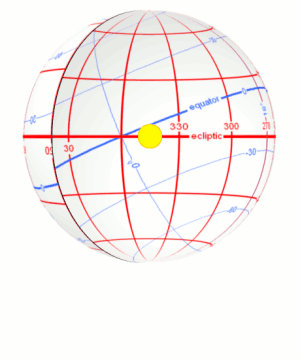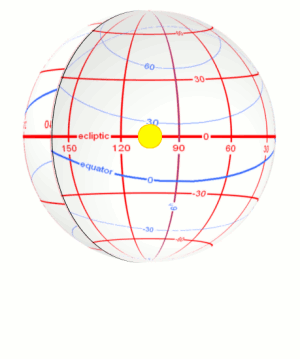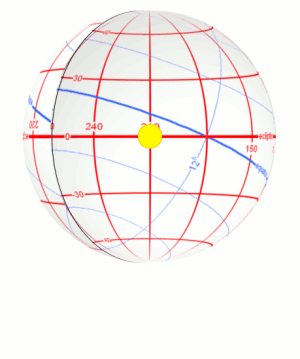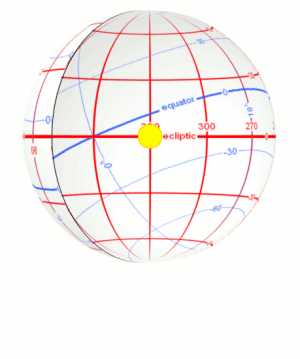 The consequence of this is the seasons because the Sun's position
to the equator changes constantly. We experience summer when the Sun is well above the celestial equator, when the Earth's northern hemisphere is pointed toward the
Sun. Conversely, when the Sun is well below the equator, when the Earth's southern hemisphere is pointed toward the sun, we experience winter.
The consequence of this is the seasons because the Sun's position
to the equator changes constantly. We experience summer when the Sun is well above the celestial equator, when the Earth's northern hemisphere is pointed toward the
Sun. Conversely, when the Sun is well below the equator, when the Earth's southern hemisphere is pointed toward the sun, we experience winter.
The ecliptic path crosses the equator at two times during the year: at the start of Spring on March 21st called the Vernal Equinox, while the other time is at the start of fall on September 21st called the Autumnal Equinox. The term equinox is derived from the word equal because at these two solar positions, day and night are the same length.
The Vernal Equinox is where we start Right Ascension, the equivalent of the Prime Meridian (Meridian of Greenwich on Earth. That point is 0h (0 hours). That position is in the constellation Pisces.
The Ecliptic Path is also basically the plane of our Solar System. Not just the Sun, but all the planets travel close to this path. The above Stellarium screen shots show the ecliptic path and the moon and various planets. Note that they all lie relatively close to the ecliptic.
Precession of the Equinoxes
 Before you can completely understand celestial coordinates, you need to have some understanding of the precession of the equinoxes which
will add a little more complexity. The more modern term is axial precession and as you hopefully will see is a better description.
Before you can completely understand celestial coordinates, you need to have some understanding of the precession of the equinoxes which
will add a little more complexity. The more modern term is axial precession and as you hopefully will see is a better description.
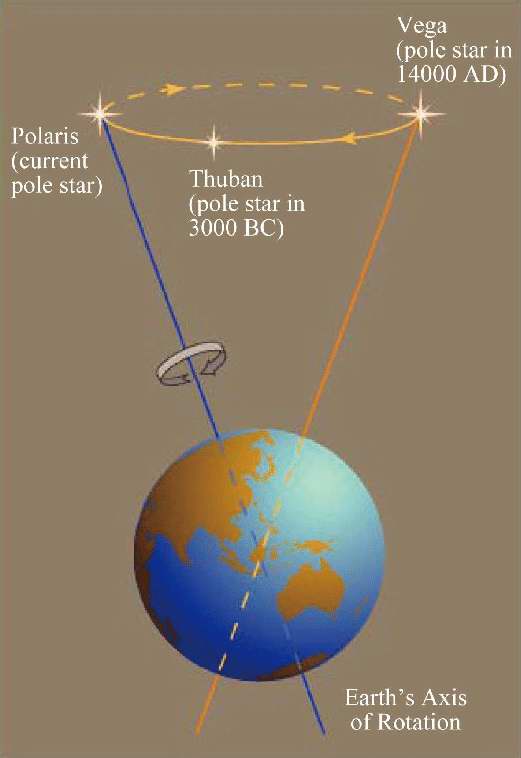 As you've seen the Earth's axis is not straight up and down as it orbits the sun but
is tilted at a 23.4° angle. The north axis of our planet points at the
north celestial pole which is a point very near Polaris (aka, the North
Star). The path the sun makes through the sky is called
the ecliptic path and it's therefore tilted 23.4°s to the celestial equator and the
two spots it crosses the equator are called the equinoxes.
As you've seen the Earth's axis is not straight up and down as it orbits the sun but
is tilted at a 23.4° angle. The north axis of our planet points at the
north celestial pole which is a point very near Polaris (aka, the North
Star). The path the sun makes through the sky is called
the ecliptic path and it's therefore tilted 23.4°s to the celestial equator and the
two spots it crosses the equator are called the equinoxes.
But the spinning Earth is also a gyroscope and our 23.4° axis wobbles (as demonstrated in the animation) over time and that period is 25,772 years. Therefore, our current "North Star" Polaris has not always been that and won't be again until another 25,772 years.
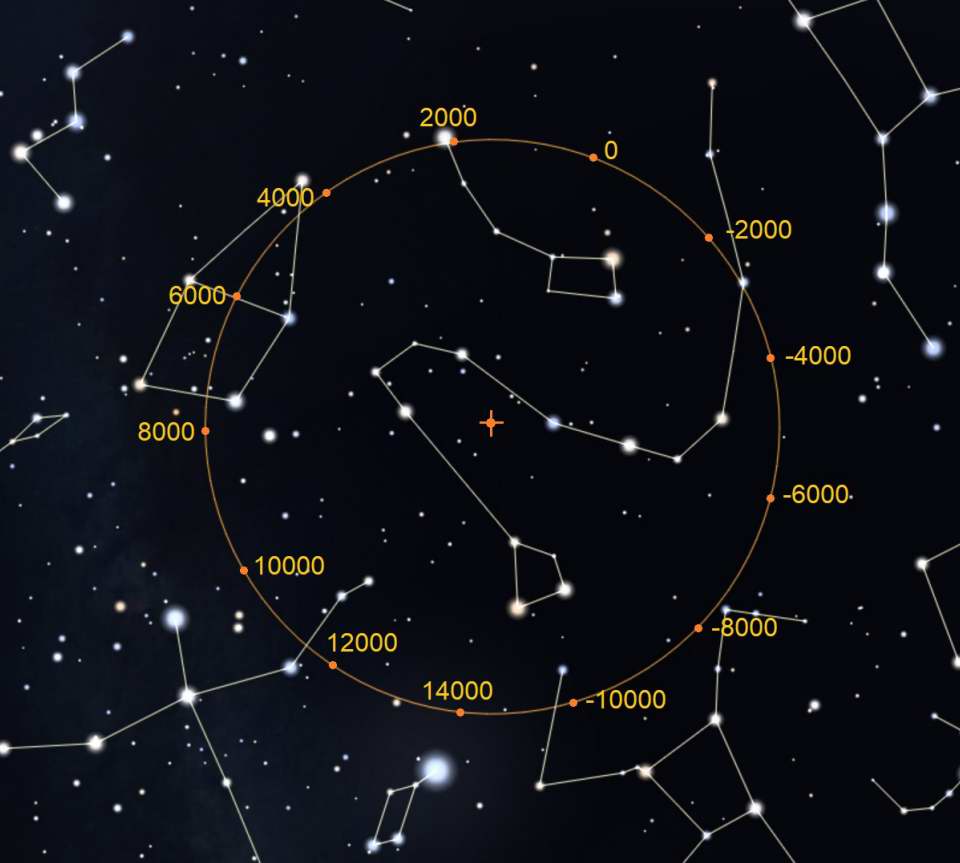 The diagram at the right shows the circle of the precession with marks to show the polar position at 2000 year intervals. The center of
the circle is the
North Ecliptic Pole. You can clearly see
that the current celestial pole is very near Polaris. But over time you'll see other stars that will become the "North Star" as this position changes.
In 12,000 years (14,000 AD) the very bright star Vega will be the north star. Also, because Earth's pole will be pointed in the opposite direction,
we'll have a complete reversal of seasons! So when we're now having summer, it will be winter.
The diagram at the right shows the circle of the precession with marks to show the polar position at 2000 year intervals. The center of
the circle is the
North Ecliptic Pole. You can clearly see
that the current celestial pole is very near Polaris. But over time you'll see other stars that will become the "North Star" as this position changes.
In 12,000 years (14,000 AD) the very bright star Vega will be the north star. Also, because Earth's pole will be pointed in the opposite direction,
we'll have a complete reversal of seasons! So when we're now having summer, it will be winter.
Granted that movement isn't very fast and to the naked-eye will take over a hundred years for it to be detected. So why does this matter? Because we don't just observe the sky without optical aid. A telescope magnifies and this motion can thus be easily seen in just years. But the effect also causes the ecliptic path to move. It has historically been called the precession of the equinoxes because it was noticed that those points slowly moved westward. And the reason that matters is we use the Autumnal Equinox as our reference for 0hr in right ascension.
J2000.0
 What this precession means is celestial coordinates are not static and they change continuously. So time becomes a very important variable.
When you see celestial coordinates you'll often see "J2000.0" along with them. It means these were the precise coordinates of an object on
January 1, 2000 and using a reference point like this is called an
epoch.
Celestial coordinates given without an epoch can be problematic.
What this precession means is celestial coordinates are not static and they change continuously. So time becomes a very important variable.
When you see celestial coordinates you'll often see "J2000.0" along with them. It means these were the precise coordinates of an object on
January 1, 2000 and using a reference point like this is called an
epoch.
Celestial coordinates given without an epoch can be problematic.
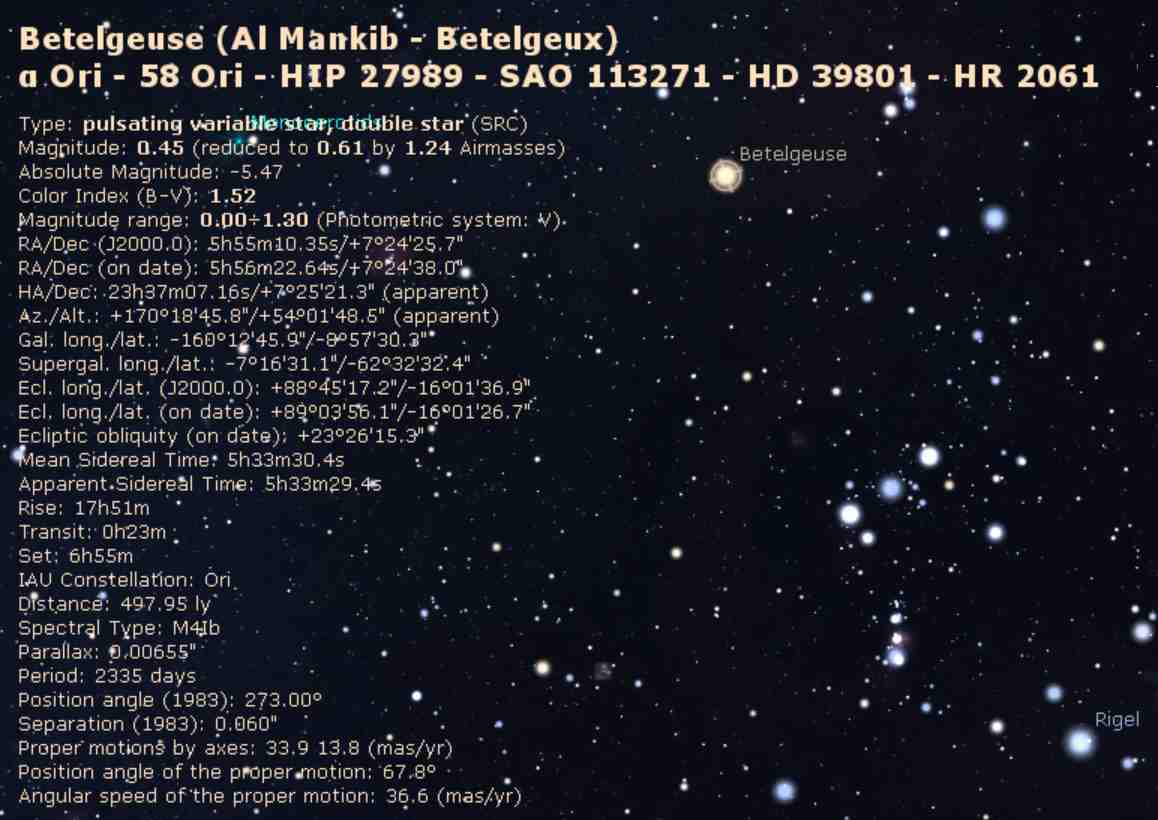
When you're viewing the simulated sky in Stellarium if you click/tap on a given star it will bring up an extensive info panel. The image at the right is a screenshot for the star Betelgeuse in the constellation Orion. In the info you will see these two lines:
RA/Dec (J2000.0) 5h55m10.35s/+7°24'25.7"
RA/Dec (on date) 5h56m22.64s/+7°24'38.0"
The first date is for the epoch and that's J2000.0. The second one is for the date which in this example was December 12, 2021. When you're viewing a screen with the time running, you'll see these figures updated continuously.