Telescope Equations
How to Size Up & Set Up a Scope
Theory

The telescope equations as presented here are quite simple, so it's entirely
possible to analyze a scope, at least to reasonable estimates, in your head --
while at the scope. It's useful to follow a consistent process, and as described
here the process goes in two steps, looking first at intrinsic properties
of the scope, then setting its operating points.
Note: for explanations of the equations below go to the Equations Summary and click on the "Explain
This" button next to the equation.
Telescope Properties
Properties that are intrinsic to the scope are those that depend only
on the objective lens or mirror.
- Find the Specifications on the Objective
Notice that there are only two values we need to completely assess
the scope and determine its operating points:
- Diameter of the objective, DO
- f-Ratio of the objective, fR
- Calculate Intrinsic Resolution & Brightness
- Resolving Power, PR = 120/DO
- Magnitude Limit, Lmag = 2 + 5 log(DO)
This can be estimated in your head. To
see how, check out the Logarithms
Page.
Operating Points
The operating points depend on the eyepieces, and it's useful to bracket
a range of eyepieces, looking for the shortest and longest focal lengths
that will be used. We will look for the high resolution end of the scale,
followed by the high brightness end of the scale.
- Highest Resolution
- Maximum Magnification, Mmax = DO
start with this because you can read it right off the scope
(or its specs) and because you may find it goes beyond the
limitations of the atmosphere,
~200. If so, you may choose to limit it to around 200, and
that in turn will influence the choice of eyepiece.
- Exit Pupil, Dep = DO/M,
where M will depend on your decision above. If you can make
use of the intrinsic max magnification of the scope (DO),
then the exit pupil will be 1mm.
- Focal Length of the Eyepiece, fe = Dep *
fR.
- Resulting Surface Brightness, SB = 2*Dep².
- Highest Brightness
- Focal Length of the Eyepiece, fe = 7 * fR
start with this because you may find that trying to reach 100%
surface brightness leads to an eyepiece focal length you can't get.
If that's the case, you choose the longest focal length you can
get, and proceed with the analysis based on that.
- Exit Pupil, Dep = fe/fR, where
fe depends on the result of your assessment above. If
you can get to the maximum required focal length then the exit pupil
will be 7mm.
- Minimum Magnification, Mmin = DO/Dep
- Resulting Surface Brightness, SB = 2*Dep², which will be
100% if you were able to get the maximum focal length eyepiece (i.e.
Dep = 7mm).
- Intermediate Points
The end points of the operating range, highest resolution and highest
brightness, serve as reference points for you. In all likelihood you
will want other eyepieces as well. These are some additional operating
points to consider:
- Half-Maximum Magnification: or twice the minimum eyepiece
focal length, which works out to twice the f-ratio and an exit pupil
of 2mm. This hits the optimum resolution spot where your eye and the
scope work best together.
- Half-Maximum Brightness: you get to this point by setting
a 5mm exit pupil, which works out to an eyepiece focal length
of 5*fR , and sets the scope to 50% surface brightness.
This is often a good compromise of magnification and brightness for
deep-sky imaging.
- Extra-High Magnification: since Mmax gets you
to where your eye can just see the smallest detail the
scope can show, you might want to go a little bigger to make
that detail easier to see. A good practice is to keep it to no
more than 50% bigger (1.5*Mmax) which means an eyepiece
focal length that is two-thirds of fe-min , which works
out to be 0.67*fR. With an exit pupil of 0.67mm and a
surface brightness of 1%, you will want to have brightness to spare
to see much detail... for example this might work when looking at
planets.
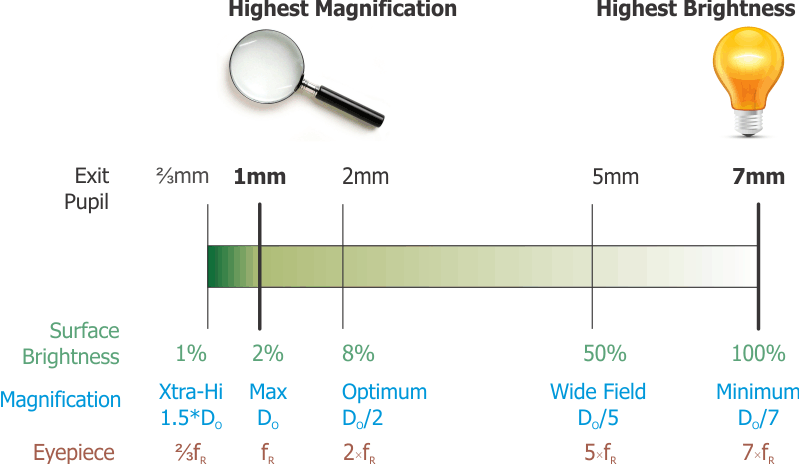
As explained on the Surface Brightness page
the range of exit pupils from 1mm to 7mm, with an extension to a Dep
of 0.67mm for pushing our luck on the high-power end, defines the performance
range for the scope as diagrammed below.
A Note on the Exit Pupil
The analysis of the operating points of the scope is conducted here entirely
using the exit pupil formulas. There are many ways to tackle the problem
and I find this to be the most straightforward, providing the most information
the fastest and with the least computation, since the exit pupil is such a
good index to performance. This is important if you want to be able to size
the situation up in your head.
Practice
Various Random Interesting Examples
I literally will just wander around the web here and provide an analysis of whatever
scopes catch my attention, to give you a sense of how the equations can work for you.
Meade ETX-80BB Backpack Observatory Telescope
 Portability of a scope can be critical, because if you can't take the scope where
you're going then it's no scope at all. This one is an f/5 with an
80mm aperture, comes with an extra-light tripod and its own backpack.
Portability of a scope can be critical, because if you can't take the scope where
you're going then it's no scope at all. This one is an f/5 with an
80mm aperture, comes with an extra-light tripod and its own backpack.
Telescope Properties
- DO = 80mm
- fR = 5
- PR = 120/DO = 120/80 = 1.5 arc-seconds
- Lmag = 2 + 5 log(DO) = 2 + 5 log(80) = 11.5
Operating Points
- Highest Resolution
- Mmax = DO = 80 is within atmosphere limits
- Dep = DO/M = 80/80 = 1mm (because we
are at max magnification, not limited by the atmosphere)
- fe = Dep * fR = 1*5 = 5mm
- SB = 2*Dep² = 2*1² = 2%
Meade claims the highest useful magnification of this scope is 160. This
analysis shows that is past the point of matching your eye's resolving
power by a factor of 2, so the resulting image would be blurry. Also,
our analysis shows you would need a Barlow doubler with a 5mm eyepiece
or else a 2.5mm eyepiece (tough to find) to double the Mmax
of 80 and get to 160x.
- Highest Brightness
- fe = 7 * fR = 7*5 = 35mm (certainly
available)
- Dep = fe/fR = 35/5 = 7mm
(because you can reach maximum brightness)
- Mmin = DO/Dep = 80/7 = 11.4
(hmm... let's discuss this, below)
- SB = 100% since we are at minimum magnification.
The brightness number comes out looking good, but the small diameter means
you get a bright image with pretty lame magnification. At a magnification
of 11.4, a good pair of 10x50 binoculars would give this scope, using a 35mm
eyepiece, some stiff competition. That means it's not likely you want to
operate there. The scope actually comes with two eyepieces, a 9.7mm and
a 26mm. Let's see what the operating point is for each.
- The 26mm Eyepiece
In order for you to get a sense for how I really do this, I will
round the focal length off to 25mm as soon as I see it's easier to divide
by an f-ratio of 5.
- fe = 26mm, call it 25mm to calculate faster with only a
4% error.
- Dep = fe/fR = 25/5 = 5mm
- M = DO/Dep = 80/5 = 16
- SB = 2*Dep² = 2*5² = 50% (they picked the half-max
brightness point)
This delivers a more decent (not awesome) magnification than the 35mm
eyepiece at a reasonable brightness. Could be useful to survey the sky,
and to show your friends a good wide-field view of things like the moon
or the Pleiades. See how rounding made it easy to do these in your head?
- The 9.7mm Eyepiece
- fe = 9.7mm, call it 10mm since that's clearly easier to
calculate with only a 3% error.
- Dep = fe/fR = 10/5 = 2mm
- M = DO/Dep = 80/2 = 40 (they picked the
half-max magnification point)
- SB = 2*Dep² = 2*2² = 8%
As mentioned elsewhere, a 2mm
exit pupil provides the optimum for the resolving power of the eye,
which makes this an interesting choice on the part of Meade. This is
probably the eyepiece you would like with this scope.
Celestron AstroMaster 114 EQ Reflector Telescope
 A bigger scope with a longer f-ratio, on a German equatorial mount (my favorite)
and excellent reviews, so let's have a look at this one.
A bigger scope with a longer f-ratio, on a German equatorial mount (my favorite)
and excellent reviews, so let's have a look at this one.
Telescope Properties
- DO = 114mm
- fR = 9
- PR = 120/DO = 120/114 = 1.1 arc-seconds
- Lmag = 2 + 5 log(DO) = 2 + 5 log(114) = 12.3
Operating Points
- Highest Resolution
- Mmax = DO = 114 is within atmosphere limits
- Dep = DO/M = 114/114 = 1mm (because we
are at max magnification, not limited by the atmosphere)
- fe = Dep * fR = 1*9 = 9mm
- SB = 2*Dep² = 2*1² = 2%
Celestron claims the highest useful magnification to be 269 -- they are using
the formula 60× scope diameter in inches, which you will see in
some references and some sites on the internet. Since it is more than double
the point where your eye sees all of the scope's detail, the images will be
very blurry, and dim with an exit pupil of 114/269 = 0.42mm and SB = 2*0.42²
= 0.4%.
The operating point we find here with a 9mm eyepiece is quite good, though,
and matches up well with the 10mm eyepiece they provide with the scope.
Along with the 10mm you also get a 20mm eyepiece which puts you at the
half-max magnification point, close to the optimum resolution. A slightly
shorter focal length of 6 or 7mm might also be handy to have.
- Highest Brightness
- fe = 7 * fR = 7*9 = 63mm -- out of practical range,
so we will have to go with something more obtainable, call it 40mm
- Dep = fe/fR = 40/9 = 4.4mm
- Mmin = DO/Dep = 114/4.4 ≈ 26
- SB = 2*Dep² = 2*4.4² ≈ 40%
The higher f-ratio limits the surface brightness you can achieve with this
scope, but gets you to maximum magnification with a reasonable eyepiece focal
length.
Seeing faint nebulas or galaxies with this scope will be a challenge. A 40mm
eyepiece gets to 40% surface brightness and yields a 26x magnification, which
is a bit low, and the 20mm eyepiece, the longest focal length provided with
the scope, has a Dep = 20/9 = 2.2mm, a magnification of M =
DO/Dep = 114/2.2 = 51, pretty decent, and SB = 2*2.2²
= 10% -- not horrible but not particularly good for deep sky observing.
Special Note: The deep-sky (brightness) vs. magnification
limitations you see with this scope and the previous one are not a reflection
against the scopes -- they are both great for what they do and have gotten great
reviews. What this is showing is the motivation that astronomy enthusiasts have
for going with larger diameter, also heavier and costlier, telescopes.
Orion SkyQuest XT8 Classic Dobsonian Telescope
 A really popular 8-inch scope on a Dobsonian mount.
A really popular 8-inch scope on a Dobsonian mount.
Telescope Properties
- DO = 203mm
- fR = 6
- PR = 120/DO = 120/203 = 0.6 arc-seconds
- Lmag = 2 + 5 log(DO) = 2 + 5 log(203) = 13.5
Operating Points
- Highest Resolution
- Mmax = DO = 203 is within atmosphere limits
(just barely)
- Dep = DO/M = 203/203 = 1mm (because we
are at max magnification, not limited by the atmosphere)
- fe = Dep * fR = 1*6 = 6mm
- SB = 2*Dep² = 2*1² = 2%
Orion claims the highest useful magnification to be 300 -- and this one
can be defended, as it aligns with the recommendation made in the "Theory"
section above.
On the other hand, the atmosphere will not allow you more than a magnification
of 200, and usually much less. So getting to a magnification of 200 with a
6mm eyepiece is likely to be all you would ever need with this scope. A 4mm
eyepiece (or 8mm with a 2x Barlow) might be interesting to use for testing
purposes, and would be less useful for observing.
- Highest Brightness
- fe = 7 * fR = 7*6 = 42mm. Period. Get one
of those for this scope.
- Dep = fe/fR = 42/6 = 7mm
by definition since we are at minimum magnification.
- Mmin = DO/Dep = 203/7 = 29
- SB = 100% since we are at minimum magnification.
Check it out -- maximum telescope brightness reached at a magnification of
29. Very decent. A 10" scope hits this point with a magnification of 36,
provided it has a low enough f-ratio (6 or less).
- Intermediate Points
- Half-Max Magnification: Dep = 2 means an eyepiece focal
length of fe = Dep*fR = 2*6 = 12mm.
- Half-Max Brightness: Dep = 5 means an eyepiece focal
length of fe = Dep*fR = 5*6 = 30mm.
Orion gives you a 25mm eyepiece with the scope, you could count that
as close enough.
- So with an eyepiece set of 6mm, 12mm, 30mm, and 42mm, you have the
full range nicely covered, all the way from the maximum magnification
allowed by the atmosphere to an image that is 100% brightness.
Pretty sweet.
Obsession Telescopes 18-inch Dobsonian
 One last example, we might as well take a look at a monster.
One last example, we might as well take a look at a monster.
Telescope Properties
- DO = 18" * 25.4 = 457mm
- fR = 4.5
- PR = 120/DO = 120/457 = 0.3 arc-seconds
- Lmag = 2 + 5 log(DO) = 2 + 5 log(457) = 15.3
Wow. Pulling in the eighth brightest moon of Saturn (Hyperion).
Operating Points
- Highest Resolution
- Mmax = DO = 457
Oh, ah... No.
No, no, no. Not on this planet, as long as we continue to enjoy a
breathable atmosphere. In this case we are going to define
Mmax to be what we think is achievable, and I would call that
200. It's a judgement call, and you might go with a different
value, the arithmetic follows the same process as here:
- Dep = DO/M = 457/200 = 2.3mm
- fe = Dep * fR = 2.3*4.5 = 10mm
- SB = 2*Dep² = 2*2.3² = 11%
Going beyond this point in magnification will simply provide a really close,
detailed view of the blurring and distortion being produced by atmospheric
conditions. Look at the surface brightness, though, at 200x: 11%, more than
5 times what the 8" gives us at that magnification. This is the point of
the bigger scope.
- Highest Brightness
- fe = 7 * fR = 7*4.5 = 32mm. Easy to get,
this would be highly recommended... interesting to note this is the
longest focal length eyepiece you should be using with this scope.
- Dep = fe/fR = 32/4.5 = 7mm
by definition since we are at minimum magnification.
- Mmin = DO/Dep = 457/7 = 65.3
Wow. This is the minimum magnification for this scope.
- SB = 100% since we are at minimum magnification.
Since the magnification is so high at maximum brightness, the deep sky images
are to die for. The Ring Nebula jumps out at you even under a full moon.
A scope like this is a deep-sky explorer's dream.
- Intermediate Points
- Half-Max Magnification: that's pretty much what we ended up picking
when we realized that max magnification would be obliterated by all
the air up there.
- Half-Max Brightness: Dep = 5 means an eyepiece focal
length of fe = Dep*fR = 5*4.5 = 22.5mm.
Televue makes a nice 22mm (I didn't say cheap) and I think Celestron's
got one as well, both with 2" barrel which would fit this scope. 20mm
is a little easier to find... in any event this operating point is
reasonably achievable.
- We're not even going to discuss extra-high magnification with this
scope. So then you're really pretty much set with an eyepiece that's
got about a 10mm focal length, one that's about 20mm, and one that's
about 30mm. More than just these three does not make a lot of sense.
In Summary...
You can see how the performance scale provides a framework that helps with sizing
up and setting up a scope.

- The exit pupil serves as a central reference point for calculations.
Always going first to the exit pupil does three things for you:
- Tells you where you are on the performance scale.
- Keeps it simple: you always know what to do first
- Positions you to quickly calculate magnification, eyepiece,
and surface brightness.
- We use the end points of the scale to bracket the operating range:
highest magnification, then highest brightness.
- We included practical considerations in the analysis: whether the
highest achievable magnification is limited by the atmosphere, and
whether the longest focal length eyepiece is decided by what's available.
- The two intermediate operating points — half the scope's maximum
magnification and half the maximum brightness — serve as
additional guideposts which help us to understand our choices of
operating points for the scope.
We didn't try to nail down an answer to five-decimal-place accuracy. We found
what eyepieces to use with the scope and how to use them. There are only so many
choices for eyepieces that are available on the market, and ultimately performance
is subjective. It will depend on the target being observed, the observing conditions
and YOU, the observer. The goal is finding where you want to be, then getting
as close as reasonable. Like a game of horseshoes, close counts.
 Back to Telescope Equations Home Page
Back to Telescope Equations Home Page
Questions
Your questions and comments regarding this page are welcome.
You can e-mail Randy Culp for inquiries,
suggestions, new ideas or just to chat.
Updated 17 May 2019
 Portability of a scope can be critical, because if you can't take the scope where
you're going then it's no scope at all. This one is an f/5 with an
80mm aperture, comes with an extra-light tripod and its own backpack.
Portability of a scope can be critical, because if you can't take the scope where
you're going then it's no scope at all. This one is an f/5 with an
80mm aperture, comes with an extra-light tripod and its own backpack. 

 Portability of a scope can be critical, because if you can't take the scope where
you're going then it's no scope at all. This one is an f/5 with an
80mm aperture, comes with an extra-light tripod and its own backpack.
Portability of a scope can be critical, because if you can't take the scope where
you're going then it's no scope at all. This one is an f/5 with an
80mm aperture, comes with an extra-light tripod and its own backpack.  A bigger scope with a longer f-ratio, on a German equatorial mount (my favorite)
and excellent reviews, so let's have a look at this one.
A bigger scope with a longer f-ratio, on a German equatorial mount (my favorite)
and excellent reviews, so let's have a look at this one.  A really popular 8-inch scope on a Dobsonian mount.
A really popular 8-inch scope on a Dobsonian mount.  One last example, we might as well take a look at a monster.
One last example, we might as well take a look at a monster. 
 Back to Telescope Equations Home Page
Back to Telescope Equations Home Page